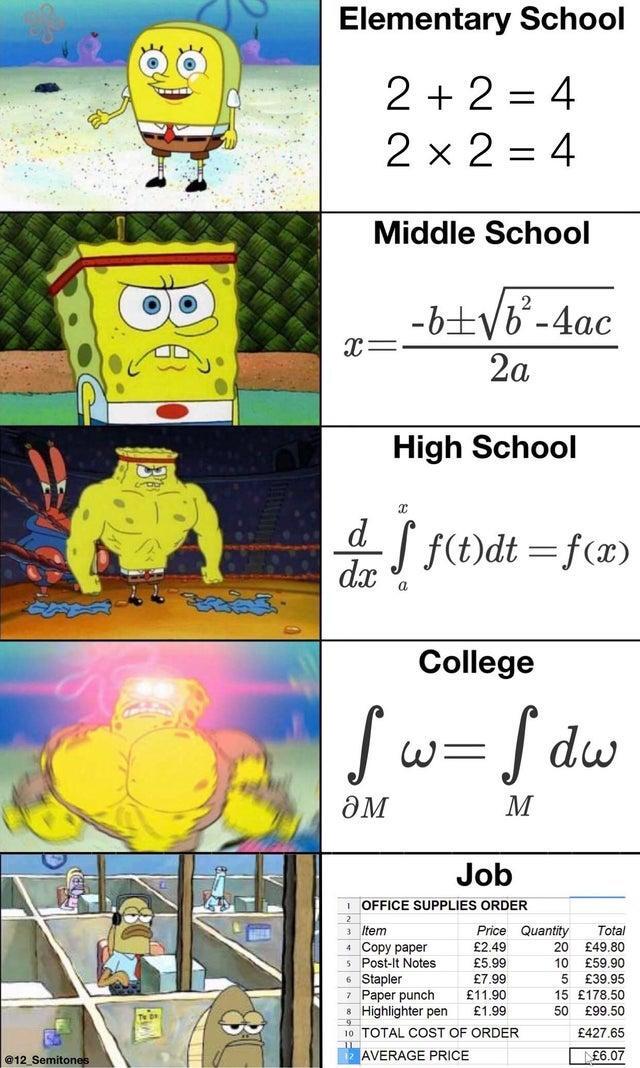YOU’RE DOING QUADRATICS IN MIDDLE SCHOOL?’
Memes
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
Yes, that's standard at least in Germany
In Spain too, it's also needed in vocational training (FP1, FP2) for carpenters, electricians, plumbers, etc., because it involves necessary calculations in their work, such as trigonometry, spheronometry, vector forces, flow calculations, among others. For office workers, naturally, percentage calculations are not overcome, but even there second degree equations can arise.

Yeah it was a middle school thing in Finland too, at least in the 90's.
I did an exchange year in the US in my 2nd high school year, and I was honestly a bit surprised at how… well, simple it all was. I was a senior in the US and I'd learned just about everything they taught that wasn't specific to the US or the English language (and even some of those…) either in my 1st year in high school or in middle school.
In my experience as an American, I've learned the same thing in multiple years, we kind of just chose a point to stop at and did that for our entire god damn school year, never moving on. We could have talked about so much interesting history, but no, we need to talk about WW2 and completely gloss over most other things for the 12th year in a row
For christs sakes I was learning FRACTIONS AND DECIMALS IN MY SENIOR YEAR
Are you sure you weren’t in a remedial school? lol
I will admit the reason my last two years were such a stark contrast to my previous years was because I went from honors down to basic because I went to a vocational high school, Diamond Oaks, and they only had the base classes
But still I never want to have another history class on WW2 again, I don't mind learning the era but I've relearned the same thing over and over again
I'm American, I definitely learned this stuff in 7th or 8th grade. Granted, I didn't use it past high school, and I forgot it before I finished college, but that's definitely when I learned it.
Bro I’m American and they didn’t even mention algebra until 9th grade, the fuck you mean quadratics in middle school
Math is personalized in American schools. There's on grade, advanced, gt, and accelerated. Each level above on grade is how many years ahead your class math is. Depending on how large your school is, gt and accelerated math students will take math with the grades above them.
On grade would be quadratic in 9th.
Idk what middle school really is because it's not been a thing at any of the schools I've been to, but it's definitely something you do a lot earlier than calculus. If calculus comes in in your last three or four years of high school, quadratics are what you're doing for at least two years before that.
Middle school is usually grades 7-8
In Hong Kong too, though the dividing is a bit different. High school is like the last 3 years of secondary school, and middle school is like the 3 years in primary school and 3 years in secondary school.
We also have vector and matrix on top of calculus in high school if you take the elective course. The compulsory part contains geometry, complex, probability, etc.
If you want, we have some samples. I took module 2. Compulsory Module 1: Calculus + Statistics Module 2: Algebra + Calculus
Yeah seriously WTF, I didn't even learn basic Algebra until freshmen year of high school! We never even got to the math with the fancy letters in it. I have no idea what those cursive f, d, and w characters mean.
Cursive big f: "integration", which can be interpreted in two ways. One is "area under the curve" for some part of the curve. Other is "average value of a part of the curve multiplied by the size of that part of the curve". Curve being the function, the graph, f(x), however you wanna call it.
Normal d: "differentiation" (from difference), infinitely small change. Usually used in ratios: df/dx means how much does f(x) change relative to x when you change x a little bit.
Cursive d: "partial", same as normal d but used when working with higher dimensional data like 3D. Can also mean "boundary" of something. Example: boundary of a volume in 3D, like wrapping paper around a box. Or, boundary of such wrapping paper itself, if it's not perfectly connecting.
Omega: just a Greek letter used as a variable, in this case there's a history of it being used as a sort of "density" variable in the field of differential geometry. The college row in the meme is kind of translating the high school row from a function to a 3D volume.
I did advanced mathematics and chose physics as one of my elective subjects in school. Nowadays, I do a lot of work based around analytics and forecasting.
"We need to find the average of this."
"That's easy. I'll do some more advanced stuff to really dial in the accuracy."
"Awesome. What's the timeframe?"
looks at million row dataset "To find the average? Like a month. Some of these numbers are mispelled words... Why are all these blank?"
"Oh, you'll have to read this 45 page document that outlines the default values."
And that's how roffice maths works. Lots and lots of if conditions, query merges, and meetings with other teams trying to understand why they entered in the thing they entered. By the time the data wrangling phase is complete, you give zero fucks about doing more than supplying the average.
Oh, sorry the 45 page document is for something else. The only person who understands this dataset is Dave and he was made redundant 5 years ago. Anyway, can you get this done today?
Dang, I was really hoping this would be one of those stories that goes like:
"How long will that take?"
"It's a lot of data...like a month?" (But I actually wrote a Python script that compiles and formats it perfectly in like 5 minutes.)
"You're such a hard worker!"
Shhhh
Yup this is every job now. Wrangling numbers. The actual job or calculation could be done in days if less. But dealing with dirty information and playing detective which isnt even part of it is the sink hole of every job right now.
If Timmy has 45 pages to read on a bus traveling an average speed of 35 mph with an mean stop distance being 0.7 kms how many stops will Timmy pass before this fucking meeting ends ?
That's software development for you. Why is that weird value there? Because some guy, at some point, had checked for that and somehow it's still relevant.
I know of a system that churns through literally millions of transactions representing millions of Euros every day, and their interface has load bearing typos (because Germans in the 90s were really bad at the Englishs).
I was denied a mathematics education, for real. I can't even do long division, nevermind that squiggly F shit. I thought that stuff was only for astrophysicists.
I want to learn basic maths, but I'm in a 'learned helplessness' mindset where I can't even get through basic sums and equations intended for children (I'm old as fuck now).
I was diagnosed with autism a few years back, which kinda made no sense. I would have expected rainman powers, but numbers just don't jive with my cunt of a brain. Maths is as inscrutable to me as people's faces or social cues.
You might also have discalcula, which is a real but somewhat uncommon thing where you're absolutely shit at math. I have no idea how to get tested for it though.
I kinda miss doing those relatively simple physics probems like finding how far something goes based on velocity and shit.
Most of the math I do at work is related to compound interest. Of all the math I believe the general public should understand, the concept of how paying interest to others is a total screw would get my top vote.
I have a co-worker who took out a car loan last week at, wait for it, FIFTY THREE PERCENT INTEREST! No concept of what that was costing her. She could only see, "I can afford the monthly payment."
(1 + r)^n and its friend 1/(1 + r)^n have been the two most important concepts in work and personal life that I've ever learned and applied.
That is usury. That cannot be legal? Oh, no, I just checked, wow, usury laws are weak af.
Sounds like predatory lending
I would agree, but it's not my life, not my money. You can't really go around telling people they fucked up every time you see it.
53%?!
Sounds like one of those shitty used car joints “no credit, no problem” that you sign your life away for a mediocre car.
As an actuarie this meme is kinda true but mostly false. I had classes on some advanced maths like ordinary differential equations that have never use on my day to day job. But, the actuarial sciences math in collage was elementary school level of abstraction compared with the real world. There's still a lot of excel tho, but I'm cool and use python (pandas) wherever I can.
AcTuArIe
As an engineer i literally use all of it daily.
As an engineer, doubt.
I guess depends on engineer
I use the college stuff maybe once a month, but still in Excel! You cannot escape the Excel!
I recently had to do linear algebra for the first time ever irl. I’ve been out of school for ~15 years. I was trying to make a rotation matrix to transform some points in 2D space. It took me a very long time to remember how it’s performed yet alone “transformation matrix” which is something I’d never heard of before. I got my code all working and was so proud, then later found that one of the r packages I was using could have just solved it all automatically :/
How the hell is "average price" useful?
Thats like buying potatoes and pork chops and saying the average price is $8.75. Technically true but practically useless.
What's the college one mean?
Stokes' theorem. Almost the same thing as the high school one. It generalizes the fundamental theorem of calculus to arbitrary smooth manifolds. In the case that M is the interval [a, x] and ω is the differential 1-form f(t)dt on M, one has dω = f'(t)dt and ∂M is the oriented tuple {+x, -a}. Integrating f(t)dt over a finite set of oriented points is the same as evaluating at each point and summing, with negatively-oriented points getting a negative sign. Then Stokes' theorem as written says that f(x) - f(a) = integral from a to x of f'(t) dt.
It's the most general form of Stokes' theorem that the integral of a differential form over the boundary of an volume and the integral of an exterior derivative of this form over that volume are the same. It covers a lot of classic formulas from the fundamental theorem of calculus to Green's theorem, Gauss' theorem and classic Stokes' theorem.
£7.99 for a stapler?!
I use trig heavily at work.