this post was submitted on 25 Jun 2025
144 points (93.4% liked)
Science Memes
15417 readers
1047 users here now
Welcome to c/science_memes @ Mander.xyz!
A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules
- Don't throw mud. Behave like an intellectual and remember the human.
- Keep it rooted (on topic).
- No spam.
- Infographics welcome, get schooled.
This is a science community. We use the Dawkins definition of meme.
Research Committee
Other Mander Communities
Science and Research
Biology and Life Sciences
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- !reptiles and [email protected]
Physical Sciences
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
Humanities and Social Sciences
Practical and Applied Sciences
- !exercise-and [email protected]
- [email protected]
- !self [email protected]
- [email protected]
- [email protected]
- [email protected]
Memes
Miscellaneous
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
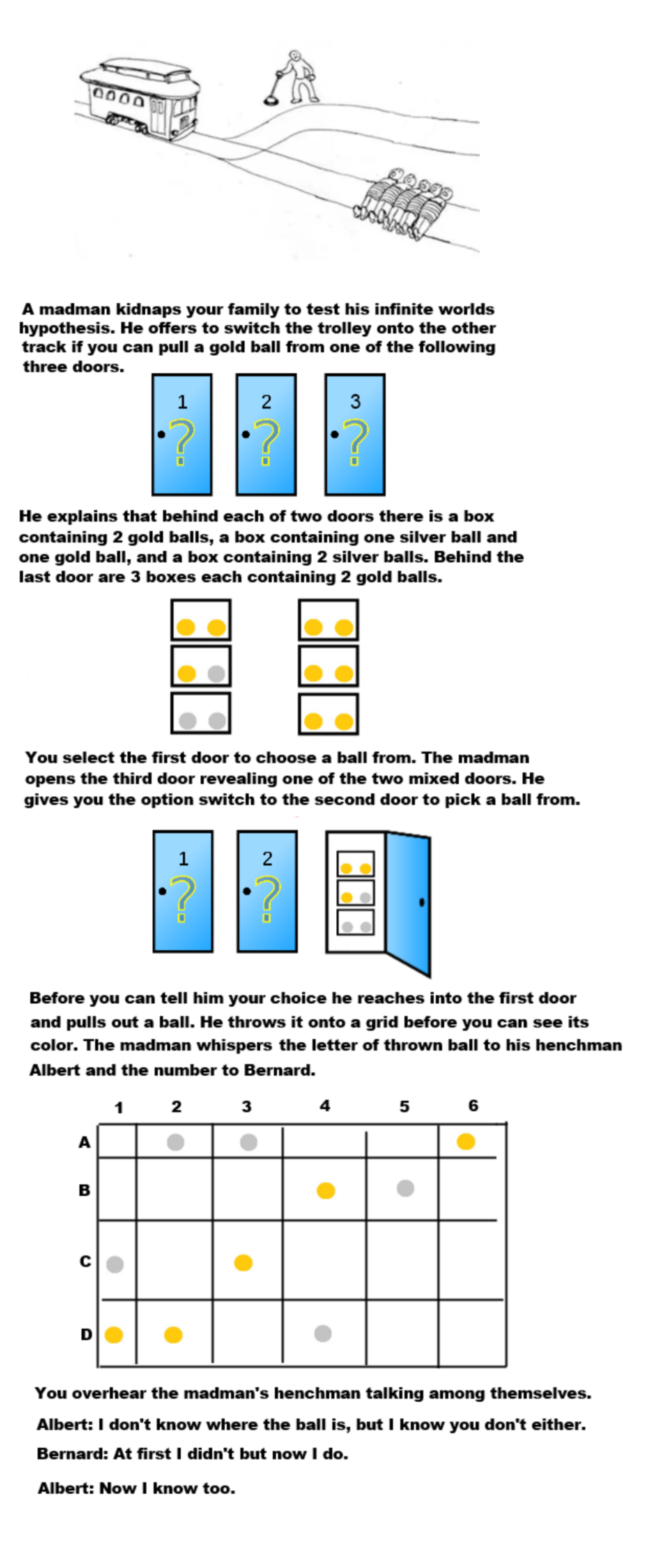
C3. I used to do these logic puzzles at work.
Both Albert and Bernard know the ball is at a certain row and at a certain column, respectively. Albert first admits two things:
This eliminates rows A and B, since B5 and A6 are the only balls in their columns. For this to work, Bernard now has to understand the above.
Then Bernard admits that now he knows where the ball is. Since we can eliminate or ignore each ball in A and B, it can either be balls D2, C3, and D4 and not any ball in column 1 using logic from #2.
At this point, Albert knows whether the ball is in C or D. If the madman told him the ball was in row C, then he would instantly know the ball is C3 given the elimination of C1 and D1. If he was told it was row D, then he still wouldn't know.
However, Albert admits the former, which tells us it's C3.