this post was submitted on 25 Aug 2024
574 points (98.8% liked)
Map Enthusiasts
3355 readers
1 users here now
For the map enthused!
Rules:
-
post relevant content: interesting, informative, and/or pretty maps
-
be nice
founded 1 year ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
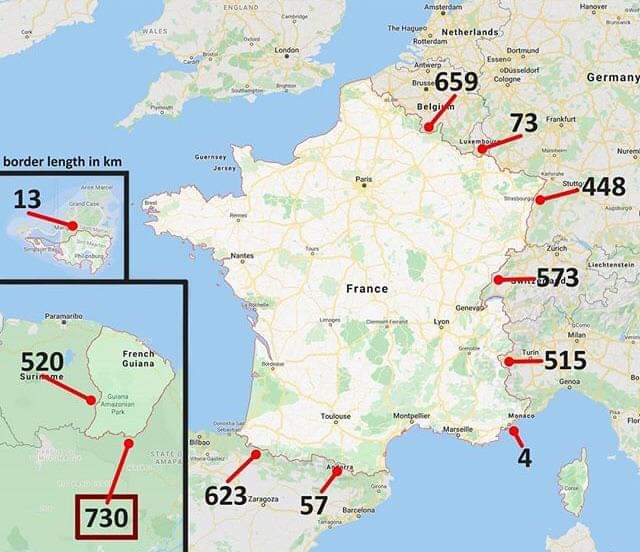
Coastlines are not self repeating and they are fundamentally finite.
I believe they were referring to this, where technically a coast could be seen as similar to fractals
https://en.wikipedia.org/wiki/Coastline_paradox
Literally from that page
Fractals are not necessarily self repeating, they just contain detail at arbitrarily small scales.
Which a physical space cannot fulfill
Fractals are not required to be self-repatiing. For example, the Mandelbrot set is a non-self repeating fractal pattern.
And please elaborate on how they are fundamentally finite.
Coastlines exist in the real world, they are by definition finite structures. You can only zoom in to them so far before the structure is no longer a coastline.
Thats making a lot of assumptions about quantum physics
An atom is not a coastline, even if it is a piece of one