this post was submitted on 27 Feb 2024
942 points (97.5% liked)
Science Memes
11448 readers
1228 users here now
Welcome to c/science_memes @ Mander.xyz!
A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules
- Don't throw mud. Behave like an intellectual and remember the human.
- Keep it rooted (on topic).
- No spam.
- Infographics welcome, get schooled.
This is a science community. We use the Dawkins definition of meme.
Research Committee
Other Mander Communities
Science and Research
Biology and Life Sciences
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- !reptiles and [email protected]
Physical Sciences
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
Humanities and Social Sciences
Practical and Applied Sciences
- !exercise-and [email protected]
- [email protected]
- !self [email protected]
- [email protected]
- [email protected]
- [email protected]
Memes
Miscellaneous
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
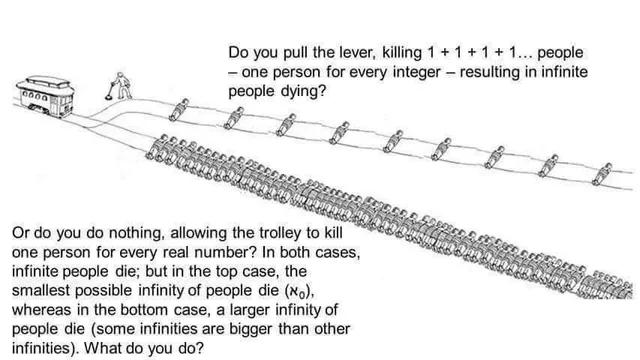
I know many people despise generative AI, but what do you think of this result from Copilot? I am bad at maths so I wonder if you experts can tell.
It's completely wrong within ZF set theory the cardinality of the integers is stricly smaller than the cardinality of the real numbers. The continuum hypothesis states that there is no set with a cardinality strictly larger than the natural numbers (or integers) and strictly smaller than the real numbers.
It accidentally kind of comes to the right conclusion, but even the conclusion isn't really correct, you don't need to be concerned with finite time since integers are a smaller cardinality.
Let's say people can be placed on a point on the track indexed by the real numbers, given any two seperate, finite, points, there would be more people packed between those two points than the entire integer track.
not an expert but the integer one is at the top i think
I'm sure if I tried to rephrase the problem getting every detail wrong, I'd do a worse job than this.
But I'd change the number of tracks.
"The cardinality of the integers is equal to the cardinality of the real numbers, which is called the continuum hypothesis."
The cardinality of the integers is not equal to the cardinality of the reals. The integers are countable (have the same cardinality as the natural numbers). A very famous proof in set theory called Cantor's diagonal argument shows the reals are uncountable (i.e. not countable).
The continuum hypothesis is also not about comparing the cardinality of the reals and the integers or naturals (since we already know the above). The continuum hypothesis is about comparing the cardinality of the reals with aleph_1.
Within the usual set theory of math (ZFC set theory), we can prove that we can assign every set a "cardinal number" that we call its cardinality. For finite sets we just assign natural numbers. For infinite sets we assign new numbers called alephs. We assign the natural numbers a cardinal that we call aleph_0.
These cardinal numbers come with an ordering relationship where one set has a cardinality larger than another set if and only if its associated cardinal number is larger than the other sets cardinal number. So, alepha_0 is larger than any finite cardinal, for example. There is a theorem called Cantor's theorem that tells us we can continually produce larger and larger infinite cardinals in fact.
So, we know the reals have some cardinality, thus some associated cardinal number. We typically call this number the cardinality of the continuum. The typical symbol for this cardinality is a stylized (fraktur) c. Since aleph_0 is countable, every aleph after aleph_0 is uncountable. By definition aleph_1 is the smallest uncountable cardinal number. The continuum hypothesis just asks if aleph_1 and c are equal.
As an aside, it is provable that c has the same cardinality as the powerset of the naturals. We let the cardinality of the powerset of a set with cardinality x be written as 2^x. Then we can write the continuum hypothesis in terms of 2^{aleph_0} and aleph_1. The generalized continuum hypothesis just swaps out 0 and 1 for an arbitrary ordinal number alpha and its successor in this new notation.
Thanks. Now I know I should avoid using LLM for anything related to maths.