This is related to the the May 16 post, but takes only the prime indexed terms. Does it still diverge?
Hint
Transform the product into a sum
Hint
The harmonic series 1 + 1/2 + 1/3 + ... 1/n +... diverges
this post was submitted on 31 May 2024
21 points (100.0% liked)
Daily Maths Challenges
189 readers
1 users here now
Share your cool maths problems.
Complete a challenge:
- Post your solution in comments, if it is exactly the same as OP's solution, let us know.
- Have fun.
Post a challenge:
- Doesn't have to be original, as long as it is not a duplicate.
- Challenges not riddles, if the post is longer than 3 paragraphs, reconsider yourself.
- Optionally include solution in comments, let it be clear this is not a homework help forums.
- Tag [unsolved] if you don't have a solution yet.
- Please include images, if your question includes complex symbols, attach a render of the maths.
Feel free to contribute to a series by DMing the OP, or start your own challenge series.
founded 6 months ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
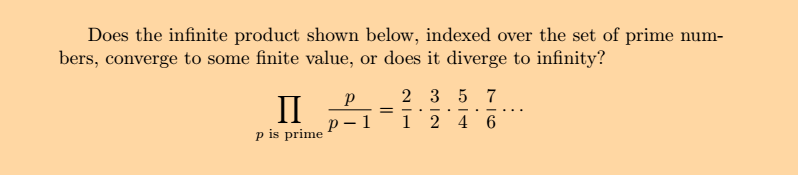
I've shown that ln(n/n-1) is always larger than 1/n, so Σln(n/n-1) for all natural number n will be larger than the series 1+1/2+1/3+...
but I don't know how to make sure the sum of all ln(p/p-1) only when p is prime is larger than the provided series
the question is strongly suggesting its divergent, i just dont know how to show it
Perhaps surprisingly, that's actually good enough since the sum of the prime reciprocals also diverges. However, I'm not letting you just assume that, and proving it is harder than the original problem.