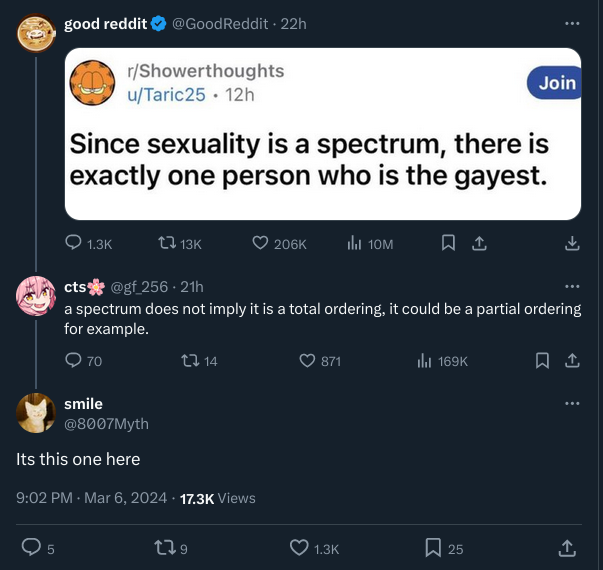
Well that's interesting: in order to define unmeasurable sets, you relied on the axiom of choice... I suppose it might be possible to define unmeasurable sets without AC, but maybe not!

Every time I encounter the axiom of choice implying a bunch of crazy stuff, it always loop back to requiring AC. It's like a bunch of evidence against AC!

I find it interesting that the basic description of AC sounds very plausible, but I'm still convinced mathematicians might have made the wrong choice... (See what i did there? 😄)

[–] [email protected] 2 points 5 months ago

It's required, but nontrivially so. It has been proven that ZF + dependent choice is consistent with the assumption that all sets of reals are Lebesgue measurable.