this post was submitted on 27 May 2024
967 points (100.0% liked)
196
16842 readers
1386 users here now
Be sure to follow the rule before you head out.
Rule: You must post before you leave.
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
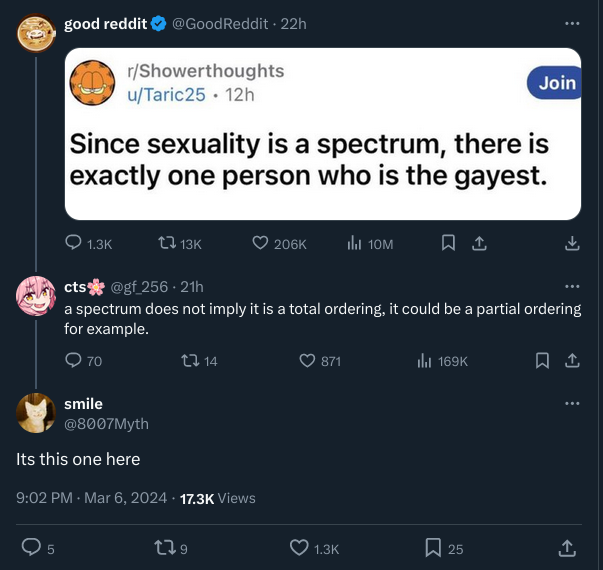
How is a spectrum supposed to not have a total ordering? To me saying sth is a spectrum always invokes an image of being able to map to/represent the property as an interval (unbounded or bounded) which should always give it a total ordering right?
It all comes down to definitions. First off, Totally Ordered is a property of the function that compares two elements not the set you are talking about. most sets have total orderings (if the axiom of choice is true then all sets have a total ordering). With Fields and vectorspaces there is the concept of a totally ordered Field which is essentially when the total ordering is compatible with it's field operations (e.g the set of complex numbers has many total orderings, but the field of complex numbers is not an ordered field).
So it really depends on how we define the sexuality spectrum. So long as it's simply a set then it has a total ordering. But if we allow us to add and multiply the gays then depending on how we define those functions it could be impossible to order the gay field.
Also a total ordering doesn't mean that there is exactly 1 maximal element (it would need to be a strict total ordering to have that property), so we can all be the gayest.
Gay field... A word I never imagined will encounter in my life