Link to comic: https://xkcd.com/2821/
I spent way too long trying to figure out why the guy and the ice cream shop were flying, and how he would move horizontally in he air...
this post was submitted on 29 Aug 2023
672 points (97.7% liked)
xkcd
8890 readers
4 users here now
A community for a webcomic of romance, sarcasm, math, and language.
founded 1 year ago
MODERATORS
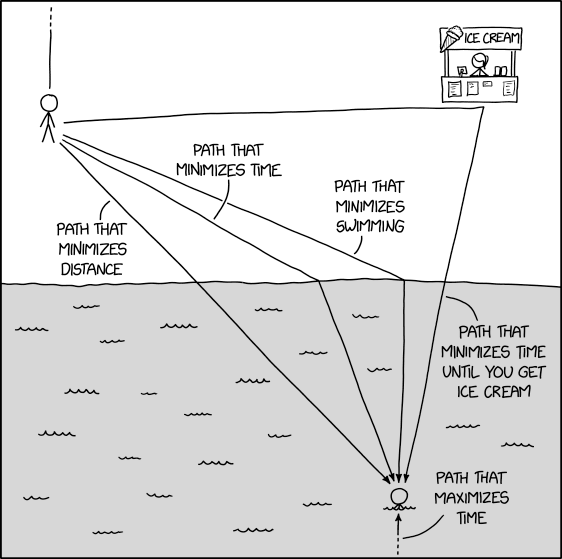
I couldn't tell what I was looking at until I searched for an explanation. All I could see was a person falling into some water past a floating ice cream stall. It's supposed to be a beach:
https://www.explainxkcd.com/wiki/index.php/2821:_Path_Minimization
"we have a beach at home"
the beach in question 
Yeah, I just thought it was two dudes racing to get ice cream first.
I was more like: but if he choses the alternative paths, he doesn't get the ice cream - that doesn't make sense! Then I understood our priorities differ.
Alt text.
Of course you get an ice cream cone for the swimmer too! You're not a monster
Now I want to see someone swimming with a cone of ice cream in each hand.
You want me to wear my swim trunks or get a bikini.. Warning before your answer: only one body type has the bouyancy to pull it off.
As an Aussie, I don't see why that is unusual. You use your feet. But if it's only two icecreams, then you hold them both in one hand and swim with the other one. All I can say about this one though is that this is a very flat beach: Waves would ruin the icecream pretty bloody fast. Must be a river or something.
Do people not swim with icecreams in other countries?
Do people not swim with icecreams in other countries?
Never heard of anyone doing it no, so probably not? 🤷
Huh. Stuff I never expected to be unique to Oz.
Swimming with something that can't get wet is not unheard of here. I sometimes swim a book over to somewhere to read, or a phone to a good place for a photo too.
See, that IS completely unheard of here! If it's not supposed to be wet, we wouldn't dream of swimming with it!
I don't know if it's because you guys are born excellent swimmers like Norwegians are with skiing, but I don't know ANYONE who wouldn't assume that swimming with something invariably means getting it wet 😄
Thanks, was disappointed about no alt text 🙏
It is simply polite to include a link to the original https://xkcd.com/2821 as per the Artist's desires.
Yes, I saw the explain, but that isn't to the actual origin.
Edited and added it. Thanks for the heads up
and I thought this had to do with light refraction lol
It does: Light does not follow the path of minimal distance between two points, but the path of minimal time. This is called Fermat's principle.
Because water has a higher refraction index than air, light is slower in it and therefore takes a longer time to travel through it. Thus, it takes less time to take a longer path that spends more time in the air.
Fun fact: The underlying law of this principle is the principle of least action. This is the most basic law of nature we know of and can be used to derive all of physics.
So... Nature is lazy?
I'd add to this that, if I'm not mistaken, it's because light takes all possible paths and the average measured time is longer
The probability of a path it takes is the sum of all possible paths. Richard Feynman uses this exact swimmer in the water example during one of his lectures of physics.
I mean, it kinda does?
Path that maximises time would be some kind of space-filling curve. Maybe it does that off panel?
Basically, yes. The path that maximises time goes around the world, so starts by going up off the top of the screen, and re-enters at the bottom.
Technically I think it could be a little longer by spiralling around the world several times, still reaching the target point despite going “in a straight line”. If we ignore the “straight line” restriction, which some of the other paths already do, then the sky’s the limit. Technically actually, the sky isn’t the limit, and the path could criss-cross over the whole planet first, and the air, and the whole galaxy, before reaching the destination as the last feasible space to arrive at. Personally I think that’s too complex for xkcd, if they are going for complex I’m sure they would have come up with something about paths through n-space and black-hole theory that is beyond my pay grade.
Xkcd good ;)
It’s the path that maximises time, not distance. Technically the path that maximises time could look the same as the path that minimises distance, they could just sit down and wait decades until a minute before they die of natural causes and then get up and head to the end, and that’s assuming that they need to arrive alive.
It would have to be a different panel but you could draw it as the whole screen being black except of the character and the destination.
If it's a space filling curve as Octoperson suggested, it wouldn't need to be big. Isn't a space filling curve infinite length if its offset is infinitesimal?
path that maximizes time? just don't move. at all
It's to do with light paths and diffraction. The time maximising path still hast to be a valid path.
If like me you can't see the picutre of the post, here is the original image:
reveal
What's up with that? I can't see any of the pictures hosted here.
I’m not positive but it might be due to the steps the Lemm.ee admin is taking to combat the CSAM uploads that have been happening and prevent the server’s administration team from being liable for potentially harmful and illegal images being hosted on their server.
Somehow he keeps on making awesome stuff, after all these years
this was our first physics lesson in year 11 in the 90s
Who could've guessed that you were training to be google maps so early?
Shouldn't the path that maximizes time have its line go through literally everywhere in the globe rather than just going around it once?
Yes, but by then the ice cream has melted
We need a calculation using the speed at which ice cream melts and the max distance he could walk.
The path that maximizes time would just be going back and forth and not approaching the endpoint.
I feel it's a missed opportunity to exclude the ice cream sales and drowning deaths correlation, but that's just me. I like the maximal time route goes up, though.
Thanks for reminding me that I have completely brain dumped all of trigonometry